
Quantum Mechanics (Physics) has revolutionized the world in general and physics in particular. This webpage, based on two lectures by Lalit A Patel, highlights the history, concepts, applications, and future of this fascinating subject, without getting into mathematical details.
Nature of Physics
Physics deals with physical items and processes. It does not deal with living beings, communalsocieties, orfinancial resources.
Physics deals with physical items and processes from physical perspective. It does not deal withtheirownership,legality, or cost.
Physics gives general principles. It does not give principles for a particular rock, planet, orlocation.
Physics gives general principles in quantitative terms. It does not talk in qualitative or vagueterms,which may besubject to interpretation.
Physics gives general principles based on or subject to observations. It does not make statementsbasedonspeculations or meditations.
Physics is an evolving science. It does not claim to be a rigid dogma dictated by someone.
Physics Prior to 1900
Physics is not a new discipline of knowledge.
More than ten millennia ago, our ancestors found that a round item can be easily rolled and can helpintransportingother items from one place to another. They also found that fire sparks can be generated by strikingtworocks. Thediscipline of physics was born out of these revolutionary inventions of wheel and fire.
For several millennia thereafter, our ancestors studied stars and planets with a remarkable accuracywith whateverlimited resources and knowledge they had. They tried their best to make some general derivations. Itisunfortunatethat some of these general derivations were misleading.
Formalization of physics as an exact science happened two millennia ago. Archimedes of Syracusestudiedfloatingobjects and derived the famous Archimedes principle, which states that weight of fluid displaced byafloatingobject is equal to the weight of the floating object. This principle was very important and a majormilestone inphysics.
Archimedes and some Chinese people studied passage of light through different shapes of glass. Thisledto thephysics of light. It also led to the invention of spectacles, a biomedical device of greatimportance.
For more than a millennium thereafter, the human civilization got busy in other pursuits. There wasnooutstandingachievements related to physics. However, this period made another significant contribution tophysics.It generateda lot of data on planetary positions and movements.
After a millennium of silence, physics roared in the fifteenth century with triumphs of the trinityofNicolausCopernicus (1473-1543), Galileo Galilei (1546-1642), and Isaac Newton (1642-1726). Copernicusanalyzedthe availabledata of planetary positions and movements. He gave a new concept of elliptical orbits and provedthatthe Earthrevolves around the Sun, which was against the old belief of heliocentric universe. Galileo carriedoutexperimentsand proved that bodies falling freely from the same height take the same time for reaching theground.Thisdemonstrated the importance of experiments and shortcomings of common beliefs. His formula forpendulumoscillationsled to an important instrument for measuring time. Newton was a genius, now known to all educatedpeoplearound theworld. His masterpiece theory of gravitational force not only explained the movements of planets andstars, but alsomade it possible to compute their trajectories with a great precision. His three laws of motion andconcept ofspectral distribution of light made physics a serious and important science.
The period of two centuries following Newton saw another great revolution in physics. Voltas andCoulombstudiedstatic electricity in frogs, thunderstorms, rubbers, and other objects. Ampere studied electriccurrents. MichaelFaraday (1791-1867) carried out lots of experiments related to electricity, and derived a connectionbetweenelectricity and magnetism. James Clark Maxwell (1831-1879) consolidated others' findings onelectricityandmagnetism in the form of four beautiful equations. Based on these equations, he made an astonishingdiscovery thatlight is a form of electromagnetic waves. He proved that light can pass through vacuum, anddisprovedthe earlierbeliefs about aether. His equations also computed the speed of light in vacuum.
These pioneering works on electricity and magnetism paved a way to the electric bulb, electricmotor,radio, phone,and many other devices, which changed the human civilization in many different ways. Physicsachieved alot during1490-1890. It achieved so much that a reputed physicist [not to be named here] commented in 1890:“Physics hasachieved everything that was to be achieved. Only thing pending is a minor explanation for theblack-body radiationdistribution.”
That physicist could not foresee the future of physics and underestimated the black-body radiationdistributionproblem.
Wikipedia article on Archimedes
Wikipedia article on Nicolaus Copernicus
Wikipedia article on Galileo Galilei
Wikipedia article on Isaac Newton
Wikipedia article on Michael Faraday
Wikipedia article on James ClerkMaxwell
Wikipedia article on black-bodyradiation
Black-Body Radiation
All substances absorb a part of radiation they get and reflect the remaining radiation. Ablack-body,such asgraphite, is a substance that absorbs almost 100% of radiation. When the black-body reaches athermalequilibrium,it emits back the radiation that it had absorbed earlier. The radiation emitted this way is known asblack-bodyradiation.
By 1890, physicists had measured intensity versus wavelength of radiation emitted by black-bodies atvarioustemperatures. They had found that for a given temperature, intensity rises almost normally withwavelength for up toa certain wavelength, and then it tapers down with wavelength. In addition to academicians,industrialists were muchinterested in understanding the black-body radiation, expecting that it would lead to betterfilamentsfor thenewly-invented electric bulb.
By 1899, several physicists presented theoretical models to explain the variation of intensity withwavelength, butthey failed miserably. Wien's model could explain the intensity variation for very high wavelengths,butit wasupside-down for low wavelengths.
In 1900, when the 19th century was about to close, a senior German physicist named Max Planck triedathen-weirdapproach to explain the black-body radiation. Prior theoretical models had implicitly assumed thatlightof a givenwavelength can have any energy value. Planck assumed that light of a given wavelength can have onlydiscrete energyvalues. He treated light as packets or quanta of energy, and assumed that each quantum has energyequalto frequencyof light multiplied by a constant value, which is now known as the Planck constant. Here, frequencyisinverse ofwavelength.
Based on this quantum theory of discrete energy levels, Planck was able to explain the black-bodyradiation patternwith a remarkable accuracy for any wavelength. This was the birth of the quantum theory.
Not many people realized the importance of this quantum theory at that very time. It took 5 yearsand agenius mindto understand and exploit its potential. It took 18 years for Max Planck to get a Nobel Prize of1918But, later isbetter than never.
Wikipedia article on black-body radiation
Illustrative page on black-body radiation
Wikipedia article on Max Planck
Nobel Prize in Physics 1918 to Max Karl Ernst Ludwig Planck in recognition of the services he rendered to the advancement ofphysicsby hisdiscovery of energy quanta
Photoelectric Effect
By about 1900, some physicists had observed that some materials emit electrons when bombarded bygammarays, whichare electromagnetic waves similar to visible light but with higher frequencies. They observed thatemission ofelectrons needs electromagnetic waves of some specific frequencies. This observation needed atheoreticalexplanation.
In 1905, while he was working in a Swiss patent office, Albert Einstein pursued his interests inphysicsin hisspare time, and published 3 research papers. The first paper on random motion of small particles wasanormalresearch paper. The second paper on photoelectric effect unraveled the potential of quantum theory,andwon him aNobel Prize in 1921. The third paper on theory of relativity brought forth many revolutionaryresults,and made himfamous as one of the greatest scientists in the history.
In his paper on photoelectric effect, he explained the observations of emissions of electrons byapplying thequantum theory. He assumed that: (1) electrons in atoms of matter are distributed in discrete energylevels, and (2)light is made of quanta of energy. Quanta of light, i.e. electromagnetic radiation, are now known asphotons.
Based on Einstein's assumptions for an electron to jump from one energy level to another higherenergylevel, aphoton (light quantum) will be needed whose energy matches the difference between the electron's newandold energylevels. If the new energy level is outside the atom, the electron will come out of the atom when itisaffected by aphoton of the required energy. Two photon of the same energy will knock out two electrons, and soon.
Einstein's this theoretical model could explain an observation which could not be explained withoutinvoking theassumptions made by Einstein. It thus provided a support to Planck's quantum hypothesis, and madethequantumhypothesis an acceptable theory. In addition to providing an explanation to an observation, Einsteinpredicted thepresence of stimulated radiation, which is a radiation emitted when an electron is stimulated to gofroma higher toa lower energy level. This prediction later on led to masers and lasers.
Wikipedia article on photoelectriceffect
Wikipedia article on Albert Einstein
Nobel Prize in Physics 1921 to Albert Einstein for his services to theoretical physics and especially for his discovery of thelawof thephotoelectric effect
Atomic Structure
By 1905, experiments had made it clear that matter is made of atoms, and atoms are made of electronsandprotons.They had not yet understood the arrangement of protons and electrons inside an atom.
Based on Einstein's discrete-energy-levels model for matter, some physicists rationalized that anatomhas protonsin the center and electrons are in some discrete energy levels.
In 1912, Niels Bohr improved the atomic model. He stated that electrons are revolving around protonsinsome fixedorbits. The first orbit can have 2 electrons; the second orbit can have 8 electrons; and so on. Theradius of anorbit and the speed of revolution of an electron are such that the outward centrifugal force of theelectron matchesthe inward electric attraction force from protons, so that there is no net inward or outward force.
Bohr's atomic model was quite understandable, and could account for most observations. Somerefinementsin the modelwere made later on to account for further observations. Bohr earned a Nobel Prize in 1922.
Wikipedia article on Niels Bohr
Nobel Prize in Physics 1906 to Joseph John Thomson in recognition of the great merits of his theoretical and experimentalinvestigations onthe conduction of electricity by gases
Nobel Prize in Physics 1922 to Niels Henrik David Bohr for his services in the investigation of the structure of atoms and oftheradiationemanating from them
Wave Particle Duality
Is light a wave or a particle? This question had puzzled and divided physicists for centuries.
In 17th century, Christiaan Huygen considered light to be waves. Isaac Newton treated light as madeofparticles. In18th century, Thomas Young allowed light from a point source to pass through two slits and collectediton a wall onthe other side. Light on the wall generated a pattern of multiple lines rather than a pattern of twosolid lines.Such a pattern could be explained only in terms of waves. In 19th century, through his famous 4equations, JamesClark Maxwell showed that light is a form of electromagnetic waves. And then, the 20th centuryintroduced thequantum theory in order to explain the black-body radiation. Max Planck had to treat light as madeofparticles,i.e. quanta or packets of energy.
Whether light is a wave or a particle remained a puzzling mystery until …
Louis de Broglie, an aristocratic noblemen, was studying physics for fun, rather than career. Hepondered over theproblem of whether light is a wave or a particle. He conjectured that light is both a wave and aparticle; it can bedescribed in both ways, as a wave and as a particle. He further conjectured that this dualityappliesnot only tolight, but it applies to everything; a thing is a thing, irrespective of whether we describe it as awave or aparticle.
In 1924, de Broglie wrote a small thesis on this novel concept of wave-particle duality. His thesiswassent toEinstein. Being a genius, Einstein could grasp the profound concept presented in the thesis. WithEinstein'sendorsement, the concept of wave-particle duality got accepted by the physics community. de BrogliewasawardedNobel Prize in 1929.
The concept of wave-particle duality solved the age-old mystery, and opened doors for a new languageinphysics.
Wikipedia article on double-slit experiment
Wikipedia article on wave particleduality
Wikipedia article on Louis de Broglie
Nobel Prize in Physics 1929 to Prince Louis Victor Pierre Raymond de Broglie for his discovery of the wave nature of electrons
Uncertainty Principle
A college teacher of mine told us a story. I do not know the authenticity or source of the story;butthe story isworth-telling here.
In 1920s. Werner Heisenberg applied to a university physics department for a postdoctoral position.Twofamousphysicists interviewed him. The first interviewer asked him a question about optical microscopes. Hecould notanswer. The first interviewer gave him a book on optical microscopes, and asked him to revisit fortheinterview.
While reading this book, Heisenberg got side-tracked. He thought deeply about optical measurementsofwaves and thenew concepts from quantum physics, and came up with the uncertainty principle. In the nextinterview, hetaunted thefirst interviewer, and narrated what he had come up with. The second interviewer, who waswell-versed inquantumphysics, immediately understood what Heisenberg was talking about, and helped him publish his workandlater on gethim a Nobel Prize in 1932.
Heisenberg's uncertainty principle states that any measurement of a quantum system disturbs thequantumsystem. Ifwe try to measure a variable of the system precisely, we cannot measure its corresponding canonicalvariableprecisely. The product of uncertainty in the measurement of a variable and uncertainty in themeasurement of thecorresponding canonical variable is at least equal to the Planck constant h divided by 2 pi.
Some of the sets of canonical variables are:
Time t and energy e
Linear position x y z and linear momentum px py pz
Angular position and angular momentum
This principle has profound implications in what we can measure and comprehend about microscopicquantumthings andprocesses. For big things and processes, the uncertainty is still there, but the uncertainty becomesinsignificantdue to large values of variables.
Wikipedia article on uncertainty principle
Wikipedia article on Werne rHeisenberg
Nobel Prize in Physics 1932 to Werner Karl Heisenberg for the creation of quantum mechanics the application of which has interalia led to thediscovery of the allotropic forms of hydrogen
Quantum Wave Function
The concept of wave-particle duality needed a mathematical language to describe waves and particlesalike.
In 1920s, while staying in a sanatorium due to his illness, Erwin Schrödinger pondered over thequantumtheory,wave-particle duality, wave propagation, and statistics, and came up with a brilliant equation, nowknown asSchrödinger equation. He got a Nobel Prize in 1933.
A typical Schrödinger equation looks like:
[i] (h bar) (d/dt) (psi) = (H caret) (psi)
Here:
(psi) is the quantum wave function of the item being described.
(H caret) is the Hamiltonian of the environment of the item.
(d/dt) is the time derivative operator.
(h bar) is the Planck constant divided by 2 pi.
[i] is the square root of minus one.
The quantum wave function (psi) is a quantum description of the item under consideration. It hascomplex, i.e. realplus imaginary, values.
A complex number and its conjugate have same-valued same-signed real parts, but same-valuedopposite-signedimaginary parts; thus, conjugate of a+[i]b is equal to a-[i]b . Multiplication of a complex numberandits conjugateis equal to sum of square of real part and sum of imaginary part; thus, multiplication of a+[i]b anda-[i]b is equalto a2+b2 .
The quantum wave function (psi) represents the amplitude of probability of existence of the item ataspace-timepoint. Its multiplication with its conjugate represents the probability of existence of the item ataspace-timepoint.
The quantum wave function (psi) varies in space and time. The space-time variation depends on theHamiltonianoperator.
What does the Hamiltonian (H caret) mean? Suppose that: you are to drive a car through somelocations;you have amap of these locations; and the map shows that region a has good roads while region b has bad roads.Then, you wouldalmost certainly predict that you will be driving fast in region a and slow in region b. TheHamiltonianis like amap, which highlights ups and downs in the space and thereby helps us predict the space variationsin(psi). Just asgovernments and map companies develop territorial maps, many physicists and chemists spend much oftheirtime indefining the Hamiltonian for various scenarios. Mathematically speaking, the Hamiltonian is a spacederivativeoperator.
The time derivative operator (d/dt) describes time variation of (psi).
The presence of Planck constant divided by 2 pi (h bar) leads to quantum effects of the item.
The presence of [i] introduces complex oscillatory behavior of (psi).
Wikipedia article on Schrödinger equation
Wikipedia article on Erwin Schrödinger
Nobel Prize in Physics 1933 to Erwin Schrödinger and Paul Adrien Maurice Dirac for the discovery of newproductiveforms ofatomic theory
Bra-Ket Notation
Schrodinger's equation in terms of a quantum wave function gave a feeling that matter isinherently of wavetype and it is of particle type only indirectly. This was not a problem for most physicists.
Quantum physics was a very hot subject in 1920s, and attracted many brilliant minds from allover the world.One such brilliant mind was Paul Dirac, a brilliant, but shy, British mathematician.
Dirac was not satisfied with Schrödinger's approach. He thought that if waves are particles,there shouldexist a particle-based description of the matter. He looked for various possibilities, andcamedown tovectors, matrices, and linear algebra.
In Dirac's approach:
<| is a bra vector, and |> is a ket vector.
<|> is a bra-ket.
< b| is a quantum state, and |b> is its conjugate.
< b|b> is a unitary matrix.
A is a matrix operator, and A* is its conjugate.
A*A is a unitary matrix.
< b|A* is A* operating on < b|, and A|b> is A operating on |b>.
< b|A*A|b> is a unitary matrix.
For example, if A* is an annihilation operator, A is a creation operator.
Dirac and Schrödinger shared Nobel Prize in Physics 1933.
Wikipedia article on Diracequation
Wikipedia article on Paul Dirac
Nobel Prize in Physics 1933 to Erwin Schrödinger and Paul Adrien Maurice Dirac for the discovery of newproductiveforms ofatomic theory
Interpretations
The core concepts of quantum physics (wave particle duality, uncertainty principle, andquantumwavefunction) were and are beyond human intuition. Many physicists have attempted to give somemeaning to theseconcepts.
The most workable interpretation of the quantum wave function was given by Max Born, who wasexpert inmathematical treatment of the physics of light. According to Born's interpretation, thequantumwavefunction (psi) represents the amplitude of probability of existence of the item at aspace-timepoint, andthe qyantum wave function's multiplication with its conjugate represents the probability ofexistence of theitem at a space-time point. Born's interpretation is able to explain the wave particledualityanduncertainty principle. Yes, Born did earn a Nobel Prize in Physics.
Richard Feynman, who is famous for his lectures on physics, gave an alternativeinterpretationin terms ofpath integrals. While Born's interpretation is in terms of existence, Feynman'sinterpretationis in termsof movements.
In order to rationalize this probabilistic nature of quantum systems, many physicists nowbelieve that whilethe actual space-time continuum has more than 4 dimensions, we human beings are confined toaspace-timecontinuum of only 4 dimensions. Similarly, many physicists now believe that while thereexistmultipleparallel universes, we human beings are confined to a single observable universe.
There is a theory known as string theory, according to which, basic building blocks of theuniverse arestrings. Roughly speaking, a string is a wave with a beginning and an end, and a string withacertainwinding pattern leads to a particle.
A typical solution of a Schrödinger wave equation is a linear superposition of pure harmonicoscillators. Apure harmonic oscillator has no beginning and no end. However, we see that each particle hasabeginning andan end. Sudarshan and Glauber were able to show that an alternative solution of aSchrodingerequation is alinear superposition of coherent states. Each coherent state is a bundle of many pureharmonicoscillators,and it has a beginning and an end. Glauber earned a Nobel Prize in Physics for thisimportantfinding.Sudarshan was not so lucky.
Wikipediaarticle oninterpretations of quantum mechanics
Nobel Prize inPhysics 1954 to Max Born for his fundamental research in quantum mechanics, especially for hisstatisticalinterpretation of the wavefunction
Nobel Prize inPhysics 1965 to Sin-Itiro Tomonaga and Julian Schwinger and Richard P. Feynman for theirfundamentalwork inquantum electrodynamics, with deep-ploughing consequences for the physics of elementaryparticles
Nobel Prize inPhysics 2005 (shared) to Roy J. Glauber for his contribution to the quantum theory of opticalcoherence
Double-Slit Experiment
If light from a point source is allowed to pass through two slits [or holes] and collectedon awall, thewall shows a pattern of multiple lines [or concentric rings] instead of two lines [or twodots].This iseasily understandable based on the wave nature of light.
Based on the concept of wave particle duality, it was predicted that if electrons from apointsource areallowed to pass through two slits [or holes] and collected on a wall, the wall should show apattern ofmultiple lines [or concentric rings] instead of two lines [or two dots].
And lo and behold, this is indeed what they observed in experiments in 1960s. Such aconfirmation of theprediction was a big step in the general acceptance of the concept of wave particle duality.
Wikipedia article ondouble-slit experiment
Experimental Validations
Experiments conducted by Davisson and Thomson found that electrons get diffracted bycrystals, and theirdiffraction patterns could not be explained without treating electrons as waves. These andseveral otherexperiments helped in the validation of the quantum physics concepts.
Nobel Prize in Physics 1937 to Clinton Joseph Davisson and George Paget Thomson for their experimentaldiscovery ofthediffraction of electrons by crystals
Quantum Statistics
Particle statistics is a way of computing the population density of various energy states.
According to classical physics, particles of the same type can be distinguished and canshare anenergystate. Particle statistics based on these classical conditions is known as Maxwell-Boltzmannstatistics.
According to quantum physics, particles of the same type cannot be distinguished.
In 1920s, Otto Stern and Walther Gerlach performed some experiments. Based on theirfindings,physicistsdetermined that particles have an intrinsic property known as spin. A particle's spin issimilarto anangular momentum, but it is fixed for a particle. Physicists then determined that photonsandcertain otherparticles have integral spin (0, 1, 2, …) and electrons and certain other particles havehalf-integral spin(1/2, 3/2, 5/2, …).
Wolfgang Pauli concluded that particles of integral spin can share an energy state, butparticles ofhalf-integral spin cannot share an energy state. Pauli earned a Nobel Prize in Physics forthisconclusionknown as Pauli exclusion principle.
SN Bose and Einstein formulated statistics for particles of integral spin. These particlesarenow known asbosons.
Enrico Fermi and Dirac gave formulated statistics for particles of half-integral spin. Theseparticles arenow known as fermions.
To understand the difference between the three types of statistics, let us see how 2particlesp1 & p2 canbe arranged in 3 states s1 & s2 & s3. With [distinguishable and sharing] classicalparticles,there can be 3double occupancies and 6 single occupancies. With [indistinguishable and sharing] bosonparticles, there canbe 3 double occupancies and 3 single occupancies. With [indistinguishable and non-sharing]fermionparticles, there can be no double occupancy and 3 single occupancies.
Wikipedia article on particle statistics
Wikipediaarticle on Stern-Gerlach experiment
Nobel Prize in Physics 1943 to Otto Stern for his contribution to the development of the molecular ray methodandhis discoveryof the magnetic moment of the proton
Nobel Prize in Physics 1945 to Wolfgang Pauli for the discovery of the Exclusion Principle, also called thePauliPrinciple
Wikipedia article on Satyendra Nath Bose
Nobel Prize in Physics 1938 to Enrico Fermi for his demonstrations of the existence of new radioactive elementsproduced byneutron irradiation, and for his related discovery of nuclear reactions brought about byslow neutrons
Illustrative example of particle statistics
Quantum Hall Effect
In 1879, Edwin Hall had found a classical physics phenomenon. If electrons are flowinginone directionand a magnetic field is applied perpendicular to the flow of electrons, then electronsaredeflectedperpendicular to the flow direction and field direction, and this deflection builds upanelectricvoltage. This phenomenon is known as the Hall effect. The ratio of the built-up electricvoltage to theinitiating electric current is known as the Hall resistance.
Around 1975, a few physicists predicted a strange phenomenon based on quantum physics.Ifelectrons areflowing through a very thin plate in a strong magnetic field in a cold environment(wherethermalvibrations are negligible), the build-up of electric voltage will be such that the Hallresistance canhave only quantized values, in multiples of Planck constant divided by square ofelectroncharge. Thisphenomenon is now known as quantum Hall effect.
In 1980, experiments conducted by von Klitzig confirmed the existence of quantum Halleffect. Theyearned Nobel Prize. Their experiment was significant and important, because it showedthatquantumphenomena are not restricted to atoms and microscopic objects as previously thought;evenlarge objectscan exhibit quantum behavior.
Quantum Hall effect has applications in measurement instruments and some electronicdevices.
Later on, some other physicists observed large-scale quantum phenomena related toexcitations inelectron fluids.
Wikipedia article onquantum Hall Effect
Nobel Prizein Physics 1985 to Klaus von Klitzing for the discovery of the Quantum Hall Effect
Nobel Prizein Physics 1998 to Robert B. Laughlin and Horst L. Störmer and Daniel C. Tsui for theirdiscovery of a newform of quantum fluid with fractionally charged excitations
Masers and Lasers
Light from an ordinary electric torch is incoherent. It gets diffracted and vanishesaftertravelingsome distance.
Masers are devices for coherent microwave radiation. Lasers are devices for coherentvisiblelightradiation. Laser is an abbreviation for Light Amplification by Stimulated Emission ofRadiation.
Radiation from a maser or a laser is so much coherent that it can travel a very verylongdistancewithout getting diffracted. No wonder why lasers have found many great applications inmanydifferentfields.
Generation of radiation in a maser or a laser is based on quantum physical photoelectriceffect. Maseror laser has a cavity with special mirrors to reflect the radiation multiple timesbefore itis sentout. This arrangement makes the radiation coherent.
Radiation from a maser or a laser displays many quantum phenomena.
Nobel Prize in Physics 1964 to Charles Hard Townes and Nicolay Gennadiyevich Basov and Aleksandr Mikhailovich Prokhorovfor fundamental work in the field of quantum electronics, which has led to theconstruction ofoscillators and amplifiers based on the maser-laser principle
Quantum Tunneling
According to classical physics, a particle thrown against a high-rise wall getsreflectedback by thewall, and therefore, cannot reach the other side of the wall.
It is not so according to quantum physics. According to quantum physics, a particle isalsoa wave. Aparticle thrown against a high-rise wall travels like a wave to make an effort to getthrough the wall.If it overcomes its attenuation while traveling through the wall, it reaches the othersideof the wall.Thus, there is a non-zero possibility of the particle overcoming a barrier and tunnelingthrough thewall.
Tunneling microscopes and many electronic devices are based on this quantum tunnelingeffect.
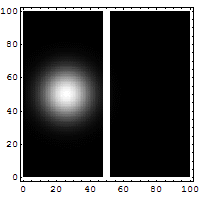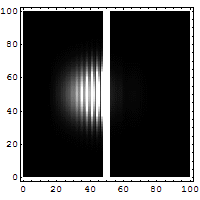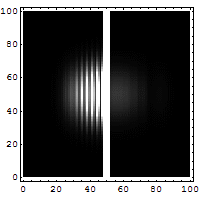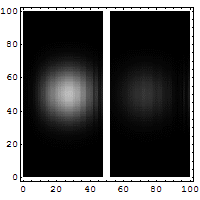
Wikipedia article on quantum tunnelling [Source of the above gif illustration.]
Nobel Prize in Physics 1973 (shared) to Leo Esaki and Ivar Giaever for their experimental discoveriesregardingtunneling phenomena in semiconductors and superconductors, respectively
Superconductivity
We all know that when electrical current flows through a conducting wire, the wire getsheated. This isbecause electrons of the current collide with matter of the wire and these collisionstendto resist theflow and convert electrical energy into heat. This electrical resistance prevents thewirefrom carryinga large current for a long time.
In 1911, Heike Kamerlingh Onnes discovered something weird. He found that if theconductingwire iscooled below a certain temperature, the wire's electrical resistance drops and becomesalmost zero. Thismeans that at low temperatures, the wire can carry large currents for long times. Quiteunderstandably,this property was named as superconductivity. Onnes was awarded a Nobel Prize in Physicsforthispioneering work.
For four decades thereafter, physicists were puzzled and could not explain the suddendropof resistanceat a certain temperature, which varied from material to material. In 1956, Bardeen,Cooper,andSchrieffer proposed a theory, which could fairly well explain the superconductivity.Theirexplanationis somewhat as follows.
Since electrons are fermions, they cannot share energy states, meaning that an energystatecannot holdmore than one electron. This non-sharing behavior at normal temperatures leads toelectricalresistance.Just as below the boiling point, vapor molecules condense to form water, and below thefreezing point,water molecules condense to form ice, {and just as above a certain age, each animalfeels anurge to getmarried,} below the superconducting temperature, electrons marry with each other to formelectron pairs.The spin of an electron is half, but the spin of an electron pair is one. Now rememberthatparticles ofhalf-integral spins are ferminons, but particles of integral-spin are bosons. Fermionscannot share anenergy state, but bosons do not mind sharing an energy state. This sharing behavior atsuperconductingtemperatures removes electrical resistance.
If a metal bar is surrounded by a conducting wire and electrical current is passedthroughthis wire,the metal bar becomes magnetic. This electromagnetism is what is behind all electricalmotors and manyother electrical machinery. At normal temperatures, magnetic field lines are inside aswellas outside amagnet. This characteristic prohibits a magnet from roaming around freely. It was foundthatatsuperconducting temperatures, magnetic field lines cannot pass inside a magnet. Thischaracteristicallows a magnet to roam around freely and to levitate as shown in the above video.
Superconductivity has lots of applications and is a great subject in itself. Forexample,MRI machinesuse superconducting magnets.
For several decades, superconductivity was possible only at very very low temperatures,below 6 degreeKelvin, that is, below -267 degrees Centigrade. Due to superconductivity's vastapplications, physicistsand chemists all over the world hunted for the superconductivity at higher temperatures.This hunt hasnow discovered superconductivity in copper oxide cuprates at temperatures as high as 133degree Kelvin,that is, -140 degree Centigrade.
Wikipedia article onsuperconductivity
Nobel Prizein Physics 1913 to Heike Kamerlingh Onnes for his investigations on the properties of matteratlowtemperatures which led, inter alia, to the production of liquid helium
Nobel Prizein Physics 1972 to John Bardeen and Leon Neil Cooper and John Robert Schrieffer for theirjointly developedtheory of superconductivity, usually called the BCS-theory
Nobel Prizein Physics 2003 to Alexei A. Abrikosov and Vitaly L. Ginzburg and Anthony J. Leggett forpioneeringcontributions to the theory of superconductors and superfluids
Wikipedia article on high-temperature superconductivity
ThePath of No Resistance: The Story of The Revolution in Superconductivity byBruceSchechter,published by Simon and Schuster, 1989
YouTube video on superconductivity-basedlavitation [Source of the above YouTube video]
YouTube video on applications and hunt for high-temerature superconductors
Josephson Effect
Let us consider two superconductors separated by an insulating plate. Let us nowconsiderthat anelectrical current is passed through one of the two superconductors.
According to classical physics, electrons cannot cross the insulator barrier and getintothe secondsuperconductor, and therefore, there will not be any electrical current in the secondsuperconductor.
Based on quantum physics, physicists thought that electrons can tunnel through theinsulatorbarrier,and these electrons would create a little electrical current in the secondsuperconductor.
In 1962, at the age of 22, Brian Josephson predicted that not only electrons but alsoelectron pairs ofthe first superconductor can tunnel through the insulator barrier, and these electronswouldcreate ahigh electrical current in the second superconductor.
This was a great prediction. It was confirmed by several experiments only within a year.Josephson wasawarded Nobel Prize in Physics for this prediction.
A circuit consisting of two superconductors separated by an insulator is known as aJosephson junction.Circuits of this type have many practical applications in devices for measurements anddiagnostics. Someinventors are thinking of designing transistor-type electronic circuits by usingJosephsonjunctions, soas to reduce power consumption and improve the performance. Stay tuned!
Wikipedia article onJosephsoneffect
Nobel Prize in Physics 1973 (shared) to Brian David Josephson for his theoretical predictions of theproperties of asupercurrent through a tunnel barrier, in particular those phenomena which aregenerallyknown asthe Josephson effects
Quantum Entanglement
Suppose a particle of zero angular momentum and zero linear momentum decays into twoidenticalparticles. According to the law of conservation of angular momentum, one of the twoparticles will haveclockwise angular momentum and the other particle will have anticlockwise angularmomentum.According tothe law of conservation of linear momentum, one particle will go in one direction andtheother particlego in the opposite direction.
Let us say that Alice measures angular momentum or linear momentum or some otherproperty ofone of thetwo particles, and Bob measures the same property for the other particle at exactly thesametime asAlice.
According to quantum uncertainty principle, measurement by Alice cannot be predictedwith1certainty, and likewise, measurement by Bob cannot be predicted with 100% certainty, andtherefore,measurements by Alice and Bob need not be correlated. However, if Alice and Bob getdifferent results,that will violate the conservation laws. It is reasonable to assume that theconservationlaws are morepowerful than the uncertainty principle. According to the conservation laws, Alice andBobshould getthe same results. If Alice and Bob get the same results, we would say that the twoparticlesareentangled. This is what is meant by quantum entanglement.
Einstein was skeptical about quantum entanglement. He called it a spooky action at adistance, which wasagainst his belief that nothing can travel at a speed beyond the speed of light.
Many experiments have been performed to find out whether quantum entanglement reallyexists.Many claimsof having seen quantum entanglement have been rejected by reviewers. However, based onclaims notdisputed so far, quantum entanglement has been noticed for distances of a few miles.
If quantum entanglement is proved to be correct, it will provide a means of secure andinstantaneouscommunication. Quantum communication is currently a great topic of research.
Wikipedia article onquantumentanglement
A recent and typical headline news about quantum entanglement
Quantum Computing
Regular computers currently in use are based on deterministic logic gates. They storeandprocessinformation in the form of bits. At a given time, a bit can have a value of either 0 or1,but neverboth 0 and 1.
Quantum computers will be based on quantum probabilistic gates. They will store andprocessinformationin the form of quantum bits, nicknamed as qubits. At any given time, a qubit can havebothvalues of 0and 1, as allowed by quantum physics principles. Only after a measurement is made, aqubitwill displaya value of 0 or 1.
Richard Feynman stressed the need of quantum computers for simulating and understandingquantumprocesses.
An algorithm is a set of steps for finding or computing something. An algorithm, whichispossible torun only on a quantum computer is called a quantum algorithm.
In 1994, David Deutsch and Richard Jozsa published a quantum algorithm, which canclassifysomeinformation much faster than a classical algorithm can do.
Peter Shor published a quantum algorithm, which can factorize a large number, a taskalmostimpossibleon a classical computer.
Lov Kumar Grover published a quantum algorithm, which can detect a needle in a large haymuch fasterthan a classical algorithm can do.
These and several other algorithms have shown that quantum computers will revolutionizetheway weencrypt and process information. Quantum computers will simplify the handling of bigdata ofhighvolume, high variety, and high velocity.
A few years back, IBM claimed that they have succeeded in building a quantum computer.Theirclaim wassubsequently rejected.
Recently D-Wave, a Canadian company, has built a computer, which they are claiming to beaquantumcomputer. Google and a few other organizations have jointly purchased one such computerforunderstanding its operations. At this stage, it is not crystal clear whether thiscomputeris truly aquantum computer.
When our future generations get quantum computers, they will laugh at our currentcomputersthe way weare laughing at those old-age computers.
Wikipedia article on quantum computing
David Deutsch's lectures on quantum computing - excellent for algorithms
FAQ on quantum computing- good for understanding applications